Метод золотого сечения и метод Фибоначчи

Метод почти половинного деления требует на каждой итерации двух вычислений значений функции: в точках и . Имеются два схожих по идее, но более экономных метода, в которых каждая итерация требует только одного нового вычисления значения функции. Если основные вычислительные усилия на каждой итерации приходятся именно на вычисление значений функции (так, как правило, и бывает), то это приводит к ускорению вычислений примерно вдвое по сравнению с методом почти половинного деления.

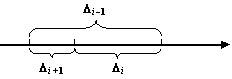
Один из методов называется метод золотого сечения. В этом методе длины последовательных отрезков ${\Delta}_i$ должны давать одно и то же число :

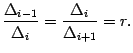
$\displaystyle \dfrac{{\Delta}_{i-1}}{{\Delta}_i}=\dfrac{{\Delta}_i}{{\Delta}_{i+1}}=r.$

Рис.9.17.Три последовательных отрезка

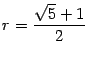При этом ${\Delta}_{i-1}={\Delta}_i+{\Delta}_{i+1}$ , откуда легко получить, что число удовлетворяет равенству . Решая это уравнение, получаем, что $r=\dfrac{\sqrt{5}+1}{2}$ . Таким образом, на первом шаге на отрезке вычисляются значения в двух точках и , расположенных симметрично на расстоянии ${\Delta}_0(r-1)$ от концов отрезка и и делящих отрезок на части, составляющие "золотое сечение". Сравнивая точно так же, как в методе почти половинного деления, значения в этих точках, выбираем в качестве либо , либо . Экономия по сравнению с методом почти половинного деления получается на всех остальных шагах, поскольку если процесс повторить на отрезке при $i\geqslant 1$ , то одной из точек деления оказывается ранее найденная точка: $l_i=r_{i-1}$ либо $r_i=l_{i-1}$ , так что одно из двух значений функции найдено на предыдущей итерации.

Ещё один метод -- метод Фибоначчи -- применяется в тех случаях, когда заранее известно, сколько итераций мы собираемся совершить, и при этом хотим получить наибольшую возможную точность в определении точки минимума. При этом оказывается, что длины отрезков ${\Delta}_i$ связаны с последовательностью чисел Фибоначчи $\{F_i\}$ , заданной начальными значениями и рекуррентной формулой $F_i=F_{i-1}+F_{i-2}$ .

Тех, кто заинтересовался этим методом, мы отсылаем за его точным описанием, как и за подробностями метода золотого сечения, к книге [Моисеев Н. Н., Иванилов Ю. П., Столярова Е. М., Методы оптимизации. -- М.: Наука, 1978].